Een verbeterde methode om de verwachte sterfte te berekenen voor Nederland
In het verleden hebben we de totale sterfte vanuit de periode 2010-2019 geëxtrapoleerd naar latere jaren, om tot een betrouwbare verwachting te komen voor de jaren 2020 e.v. We gaan deze methode verfijnen en kijken wat de consequenties zijn. We gaan nu Mannen en Vrouwen apart bekijken en de aantallen overledenen per 100.000 van betreffende groep bekijken.
Dat doen we voor drie situaties:
Totaal over alle leeftijden;
Cumulatie van de totalen van alle vijfjaarsperioden (22 groepen);
Cumulatie van de uitkomsten van alle leeftijden (106 groepen, laatste leeftijd is 105 en ouder).
Data komt van CBS
CBS heeft binnen Statline functies die de benodigde gegevens opleveren.
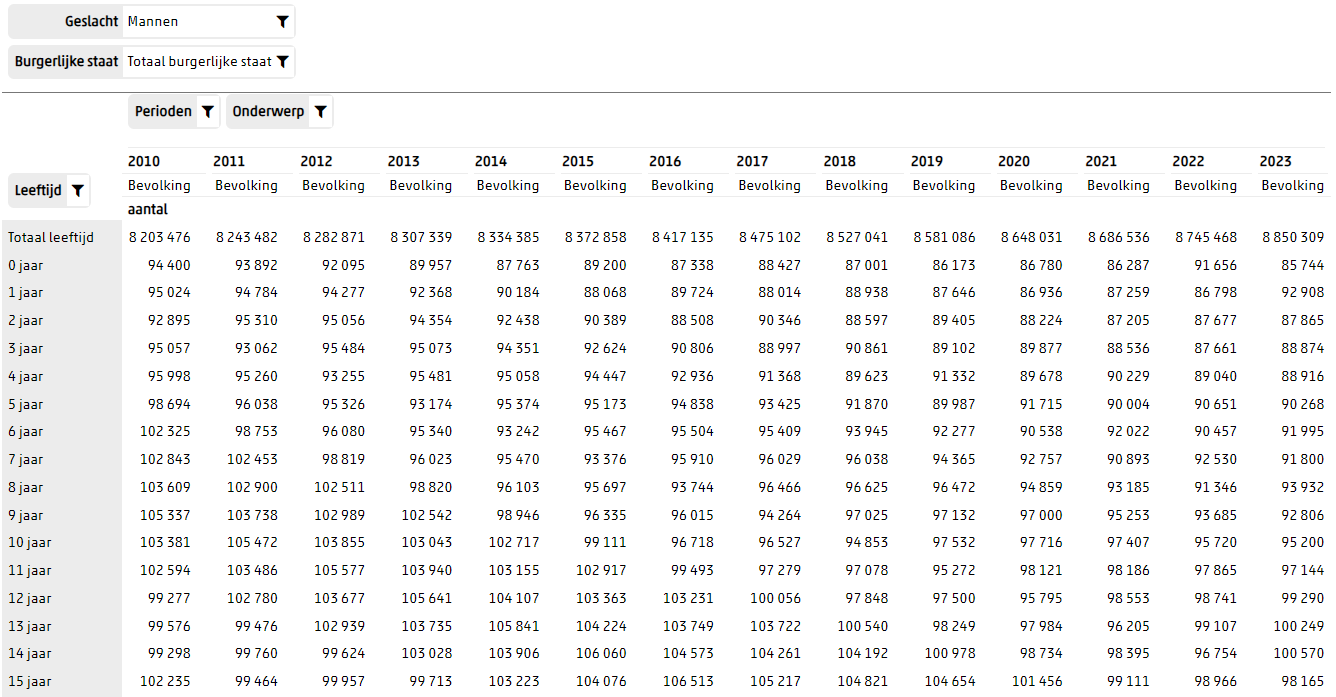
De bevolkingsomvang per leeftijd (op 1 januari van jaar X) vinden we hier. Een voorbeeld hoe dat eruit ziet, na de gewenste aanpassingen zodat we periode 2010-2023 zien voor zowel mannen als vrouwen (dit voorbeeld mannen):
We hebben de data nodig van 2010 tot heden. Deze tabel geeft de data t/m 2023. CBS geeft ook prognoses voor de bevolkingssamenstelling vanaf 2024 tot vér in de toekomst. Die prognose is gebruikt om de verwachte sterfte in 2024 te kunnen berekenen.
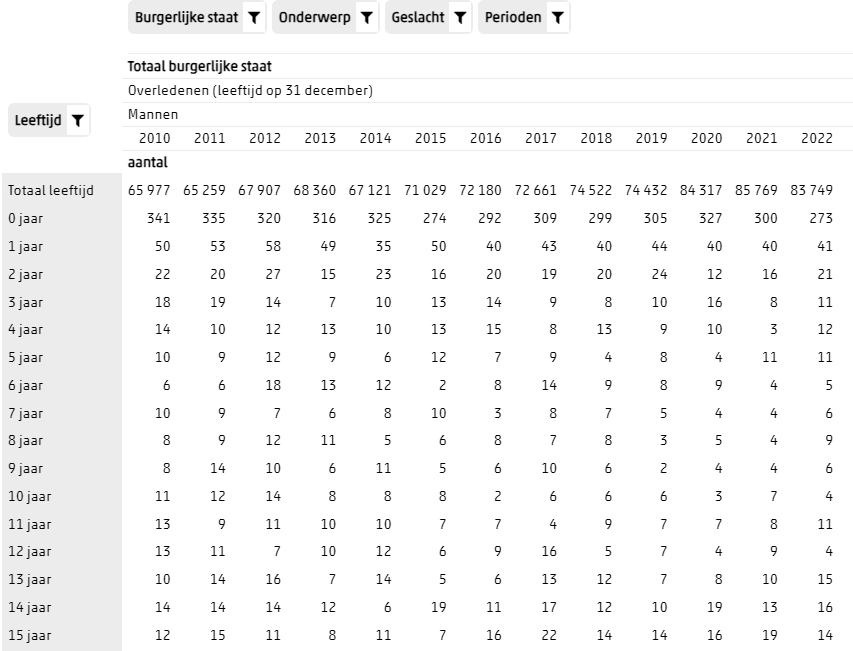
Voor het aantal doden is er deze tabel, die er na wat aanpassingen als volgt uit ziet (weer voorbeeld mannen):
We hebben nu de aantallen mensen binnen de leeftijdsgroep én de aantallen doden binnen dezelfde groep. Daarbij moet wél bedacht worden, dat iemand die is overleden op 31 december 51 zou zijn geweest, op 1 januari van dat jaar 50 was. Dat geldt in de meeste gevallen, alleen niet voor iemand die precies op 1 januari geboren is. De fout die je dan maakt is ten hoogste 1/365.
Situatie 1: Totaal over alle leeftijden
De totale sterfte per 100.000 kunnen we gemakkelijk berekenen voor mannen en vrouwen afzonderlijk door van de eerste regels in bovenstaande tabellen uit te gaan.
Als we het aantal overlijdens vermenigvuldigen met 100.000 en delen door het totaal aantal mensen, krijgen we het sterftecijfer per 100.000 voor ieder jaar, van 2010 t/m 2022. Vervolgens gaan we met de Excel-functie “voorspellen” op basis van de 10-jarige reeks 2010-2019 kijken was voor ieder jaar de voorspelde sterfte zou zijn geweest per 100.000. De uitkomst is een rechte lijn, die ook gebruikt kan worden voor het berekenen van de verwachte sterfte in toekomstige jaren. Simpelweg door het vermenigvuldigen van het verkregen getal met de bevolkingsomvang en dat weer delen door 100.000. De op die manier verkregen waarde voor de verwachte sterfte zal als je die per jaar uitzet, niet op een rechte lijn liggen omdat de bevolkingsomvang ieder jaar anders is en niet met gelijke aantallen toe- of afneemt.
Situatie 2: Cumulatie van de totalen van alle vijfjaarsperioden
We gaan nu per leeftijdscohort van vijf jaar de bevolkingsaantallen en overledenen sommeren. Bedenk wel dat als je de doden tussen 50 en 55 jaar wilt beschouwen, je naar de bevolkingsomvang moet kijken tussen 49 en 54 jaar. Ook nu kijken we weer naar mannen en vrouwen afzonderlijk.
Per cohort:
Wordt nu eerst de sterfte per 100.000 berekend.
Vervolgens wordt met de functie “voorspellen” een lineaire trendlijn berekend die voorspelt wat de verwachte sterfte is per 100.000.
Die wordt vertaald in de verwachte sterfte voor het cohort.
Om nu de verwachte sterfte voor de gehele bevolking te krijgen wordt per jaar over de 22 cohorten de verwachte sterfte gesommeerd. Door de uitkomst van de sommatie te vermenigvuldigen met 100.000 en te delen door de bevolkingsomvang wordt de sterfte voor de gehele bevolking per 100.000 verkregen.
Situatie 3: Cumulatie van de totalen van alle leeftijden
We gaan nu per leeftijd de bevolkingsaantallen en overledenen bekijken. Bedenk wel dat als je de doden van 50 jaar wilt beschouwen, je naar de bevolkingsomvang moet kijken van 49 jaar. (NB bij 0 jaar kijken we naar 0, bij één jaar ook.)
Per leeftijd:
Wordt nu eerst de sterfte per 100.000 berekend.
Vervolgens wordt met de functie “voorspellen” een lineaire trendlijn berekend die voorspelt wat de verwachte sterfte is per 100.000.
Die wordt vertaald in de verwachte sterfte voor de leeftijd.
Om nu de verwachte sterfte voor de gehele bevolking te krijgen wordt per jaar over de 106 onderscheiden leeftijden de verwachte sterfte gesommeerd. Ook nu kijken we weer naar mannen en vrouwen afzonderlijk.
Door de resultaten van de drie situaties voor mannen en vrouwen bij elkaar op te tellen, krijgen we de waarden voor de gehele bevolking.
Resultaten
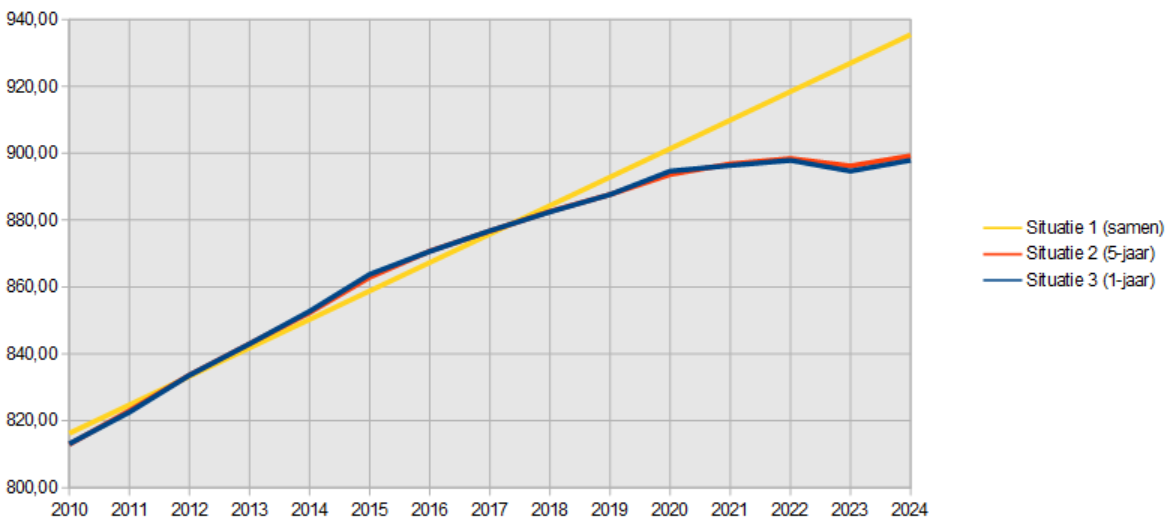
Hoe ziet de verwachte sterfte er uit? Allereerst de sterfte voor de gehele bevolking per 100.000:
De gele lijn is volledig recht, de twee andere zijn gekromd en lijken te stabiliseren nabij de 900. Dat zou betekenen dat het effect dat we steeds meer ouderen krijgen met als gevolg daarvan hogere sterftecijfers, minder belangrijk wordt. Natuurlijk wordt dit getal ook beïnvloedt (verlaagd) door immigratie van overwegend jonge mensen.
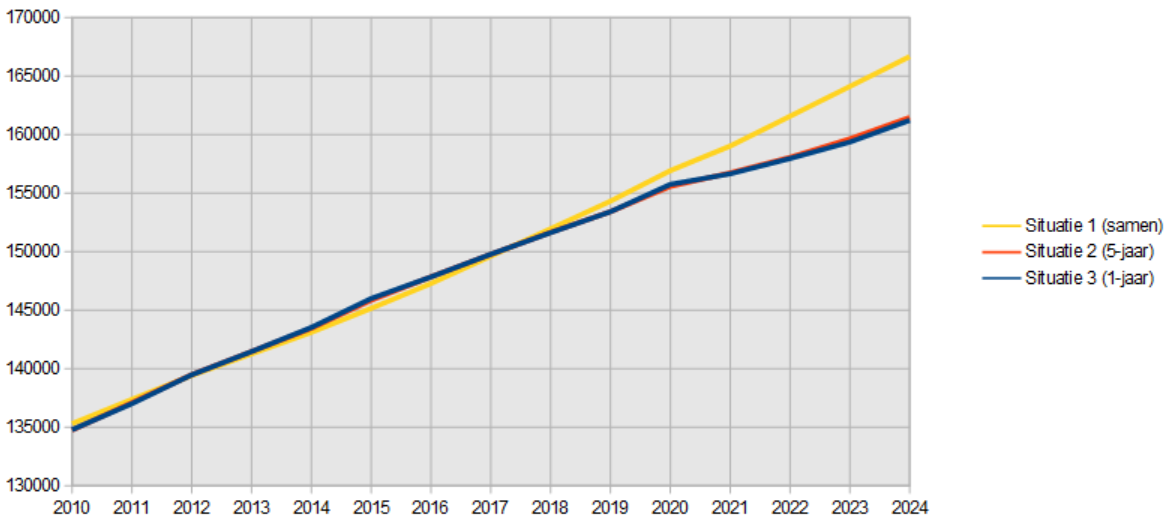
Voor de absolute sterfte komt er volgend plaatje uit:
De gele lijn is nu bijna een rechte lijn, maar nog altijd meer een recht lijkende lijn dan de rode en de blauwe. De stijging van de jaarsterfte lijkt vanaf 2015 af te zwakken, echter in 2023 en 2024 begint deze weer toe te nemen door de grote bevolkingsaanwas in de laatste jaren vnl. door immigratie en het Oekraïne-conflict.
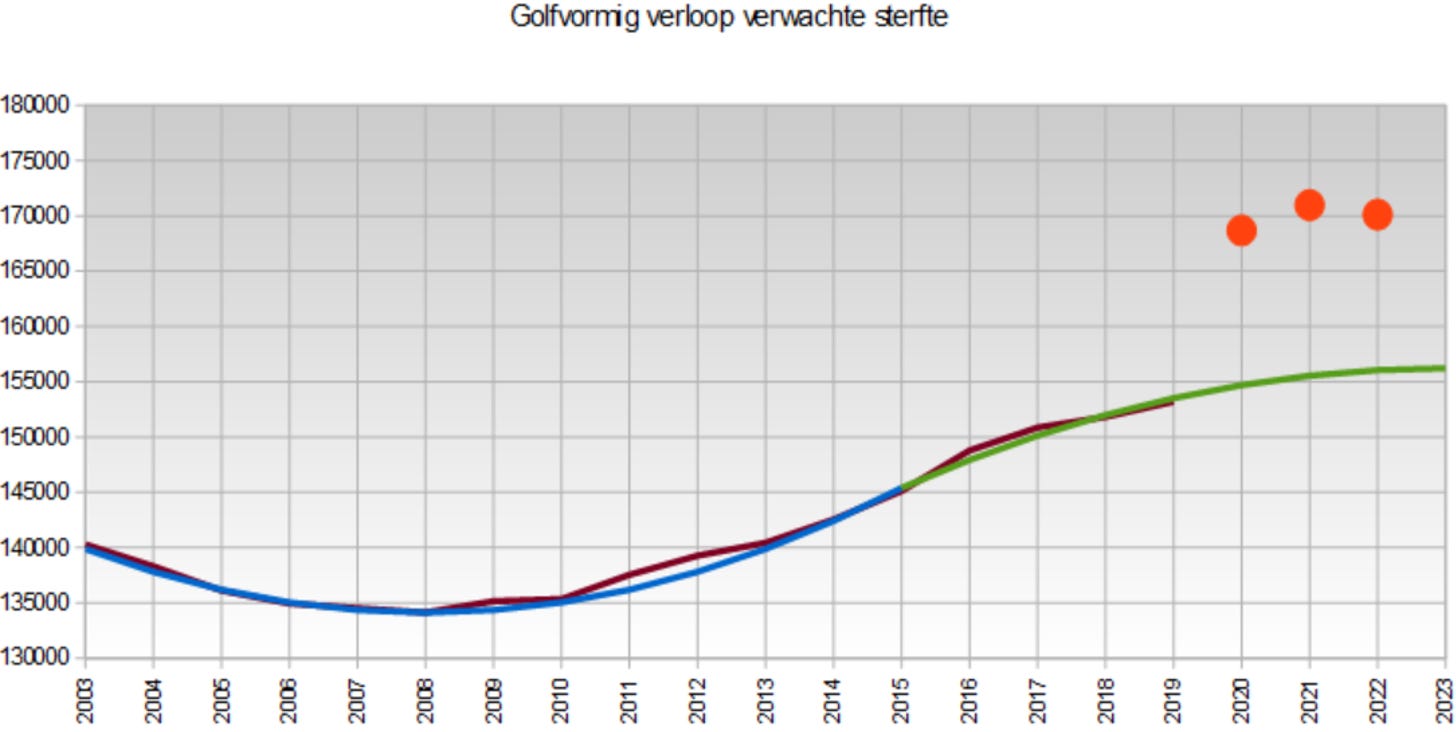
Op 2 juli 2023 publiceerde ik deze post waarin na 2015 een afname van de stijging van de verwachte sterfte wordt verondersteld. Hier het plaatje uit die publicatie:
In het in deze publicatie beschreven model laten zowel de blauwe als rode lijn zien, dat vanaf 2015 t/m 2021 de verwachte sterfte jaarlijks minder is gestegen dan het jaar ervoor. De groene lijn in bovenstaand plaatje geeft dit ook weer, al zou die vanaf ‘21 weer moeten gaan stijgen.
Berekening verwachte sterfte op basis van één- of vijfjaars model?
Het is duidelijk dat het model van situatie één (de gele lijn) leidt tot een te hoge waarde van de verwachte sterfte. Voor 2024 zou deze 166.647 personen bedragen, terwijl het model met cohorten van vijf jaar uitkomt op 161.448. er per leeftijd op 161.209. Dat is voor beiden meer dan 5.000 verschil met de eerste waarde, terwijl het onderlinge verschil van de laatste twee iets minder dan 250 bedraagt.
Gegeven het feit dat de overledenen bij een samenstel van vijf jaar minder toeval kent dan bij één leeftijd, heeft het de voorkeur om per vijf jaar te kijken. Daarmee zou de tweede situatie dus de voorkeur verdienen. Het is wél aan te bevelen om per vijfjaarscohort te kijken naar de correlatie tussen de werkelijke sterfte en voorspelde sterfte en op basis van zo’n analyse een betrouwbaarheidsinterval samen te stellen.
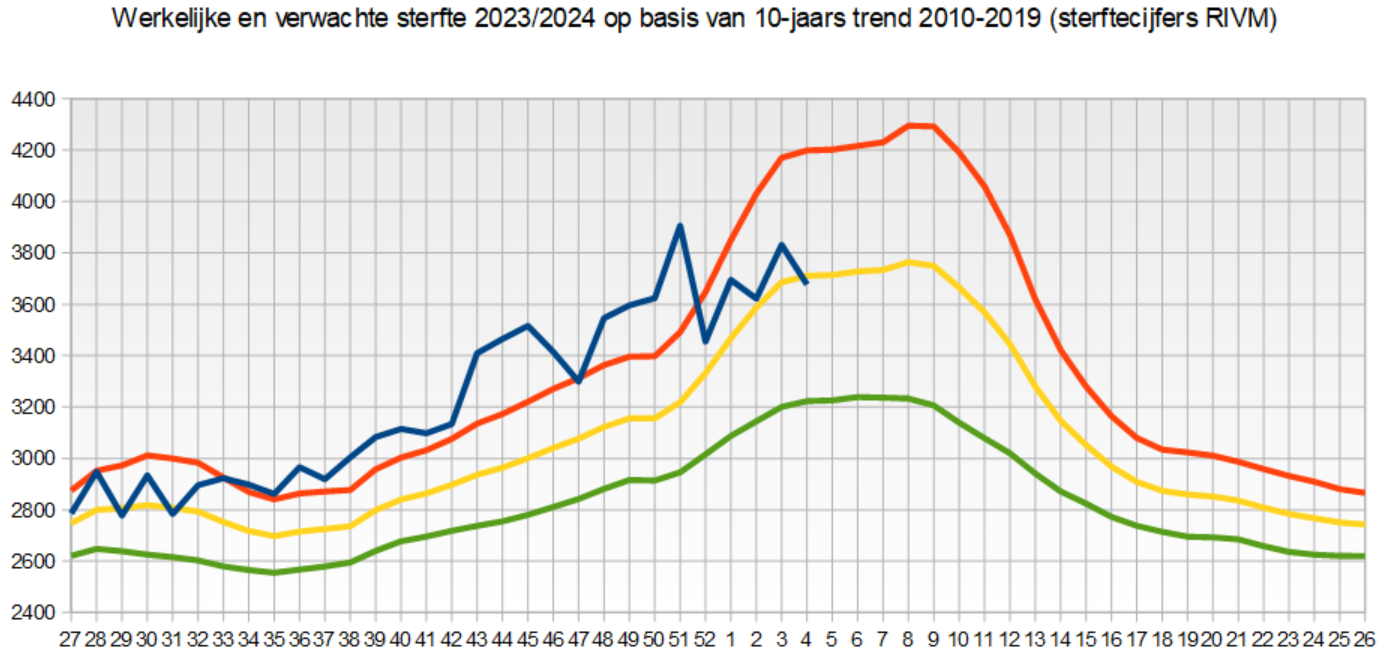
Met behulp van het verloop van de weeksterfte gedurende de periode 2019-2019, is de verwachting over het jaar - de gele lijn - te construeren, met daarbij de onder en bovengrens (groen resp. rood). De blauwe lijn geeft het werkelijke verloop van de sterfte weer op basis van de laatste (31-01-2024) cijfers van het RIVM.
Zowel CBS als RIVM gaan voor 2024 uit van een flink hogere verwachting.